ex85 中间体的优化

本节主要给大家介绍一下中间体计算的具体流程。

计算中间体前的准备：

1）催化剂表面模型的结构以及性质自己多多了解；表面原子排列，谁带正电荷，谁带负电荷，原子间距等等，这些基本的东西自己心里要有数；没事可以整理到表格或者ppt里面，方便以后写文章用；

2） 表面上可能发生的反应路径，各个基元反应，自己列举出来，整理归类方便以后分析。

3）反应路径中各种可能分子的吸附结构先优化完成，通过这些基本分子的吸附能，吸附结构，对体系大体了解一下，一方面参考文献中别人提到的反应路径，另一方面添加自己认为可能的情况。

关键点：

中间体的优化和前面我们讲到的分子或者原子在表面上的优化是一样的。意思就是计算分子吸附的时候，基本的操作同样适用于中间体的优化。可以分布算，先从粗糙的精度出发，然后慢慢提高精度。注意的一点：

对于计算速度的影响：

1） KPOINTS：先把slab固定住，用（1x1x1）的K点对刚刚搭建的中间体结构预优化一下（基本上跑个NSW = 60就差不多了）得到一个理想的初始结构，然后再增加K点密度，放开slab的表层原子，继续优化；

2）EDIFF，EDIFFG：这两个参数主要影响电子步和离子步的步数，当我们用低密度的K点进行计算的时候，电子步很快收敛，离子步收不收敛我们也不在乎，所以在这一步的时候，不用对这两个参数太较真；关键在于增加K点后，我们选取一个什么样的标准，既得到理想的结构和能量，也避免了服务器做无意义的计算；

3）ISPIN：体系需要考虑磁性的话，粗优化的时候，可以先关掉。后面提高精度后，记得加上就可以了。

4）NCORE等并行参数也不要忘记加上，详细参考：

熟练掌握不同精度下这几个参数的使用，可以极大地提高你的计算效率，节省机时。前面说的这些，基本上试用大部分的体系，但还是要靠大家自己多多测试，摸索一下最适合自己体系的方法。

本节主要取表面上：CH3OH —> CH3O —> CH2O 这两步来简单介绍，下图中圈出来的两步；其他的路径照着葫芦画瓢就行了。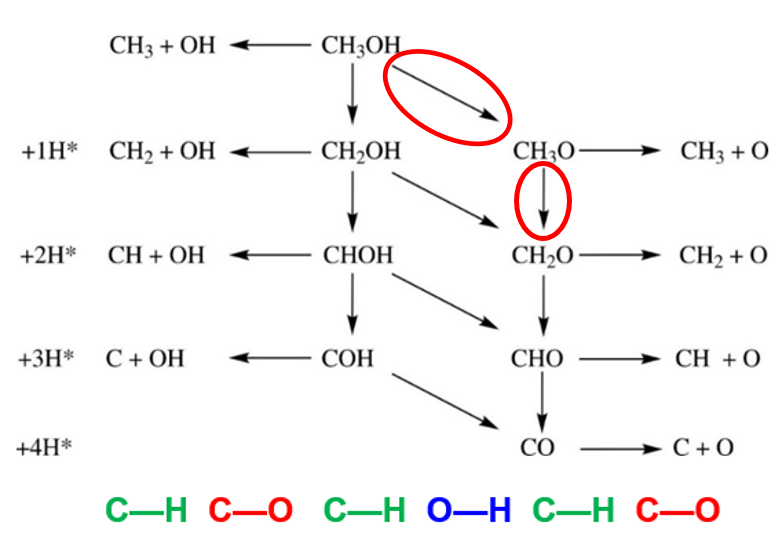

第一步：CH3OH —> CH3O + H

1）反应产物为表面上的甲氧基（CH3O*）和氢原子（H*)， CH3O* 可以继续进行C—H键断裂，或者C—O键断裂，生成CH3*+O 或者CH2O\ + H*。

注意：这里你应该可以想象到反应网络的复杂性，从一个反应物出发可以有多个不同类型的基元反应，产物作为下一步的反应物，也会有不同类型的反应，导致整个反应网络变得越来越复杂，最后交叉合并，汇总到最基本的分解产物上来。这里我们用的是甲醇，当分子C链增长的时候，基元反应的数目就会急剧增加，增加到我们挨个算不能完成的情况，这也是我们为啥要研究BEP关系的原因。另一个原因就是，成千上万个反应，整天瞎算过渡态，有时候你并不会学到太多新鲜事物，只是重复搬砖的工作，对我们以后的成长不利。

2）H原子的吸附，我们就跳过吧，相信大家经过前面的学习，应该都会了。计算CH3O的结构，我们可以从CH3OH的POSCAR出发，进行下面几点思考：

A) 删除POSCAR中对应H原子的坐标，保存为新的POSCAR，即表面上只有CH3O，提交任务进行优化；

B) CH3OH的结构中，O是在一个top的位置上，但O—H 键断裂之后，O的成键能力增强了，还会继续呆在top位置上么？所以，我们要把OCH3挪到bridge, hcp, fcc 位点上，得到几个不同的结构，提交任务进行优化；

C) 前面我们的结构OCH3是斜着在表面上；会不会有直立的结构？ OCH3是通过O与表面结合，我们是不是可以参考O原子在表面的吸附结构；搭建OCH3直立的吸附结构？

D）前面说的这几点，我们都可以通过前面所说的关键点，用一个粗糙的模型扫描一遍。然后大致分析下结果，然后进行下一步的计算，最终得到稳定的OCH3在表面上的稳定结构。

第二步：CH3O —> CH2O + H

这一步，从甲氧基进行了一步C—H反应，得到了甲醛和H。H的话继续跳过；甲醛的话，这里我们应该也需要跳过；因为甲醛是一个分子，在计算中间体前的准备这一步中，我们应该已经完成。安全起见，我们也列举一下几点需要注意的结构搭建工作：

1） 甲醛分子以C，以O还是C=O双键与表面结合？

2） 以不同部分与表面结合的时候，会在哪个位点上？

3）垂直？斜着，还是平行吸附？

总之，尽可能多思考不同的表面结合方式，采用粗糙的模型快速进行筛选，也要实时思考，粗糙模型会不会对这样的快速筛选产生影响？会不会漏掉什么可能的结构？

后面的过程依次类推，直至甲醇分子分解为最基本的化学单元(H，C, O)。

---

下面介绍另外一种中间体模型，首先回顾一下上面搭建CH$_3$OH—> CH$_3$O + H这一个反应中间体的过程：（这里我们先定义这个中间体模型为：A）

1) 从CH$_3$OH的POSCAR出发，

i) 删除POSCAR中与O相连的H原子的坐标，此时表面上只有CH$_3$O的结构，且CH$_3$O位于top位上；

ii) 稍微修改一下OCH$_3$的结合位点，尝试一下附近的hcp，fcc，或者bridge位点上CH$_3$O的结构，并分别保存到不同文件夹里面；

iii) 提交任务计算，并对比不同OCH3结构的能量，取最低的那个。

iV) 第ii）步中我们暴力直接删掉H原子，基于的假设是一旦O—H键断裂后，产物之间（CH$_3$O, H）互不影响。

另外一种中间体模型（设为：B）长什么样子呢？

1） OCH$_3$的结构与前面A的模型一样，有top，fcc，hcp，bri各种尝试的结构；

2） 除此之外，CH$_3$OH 中与O相连的H也在OCH$_3$ 附近。

也就是说，在A 模型中，我们直接删掉H原子，而在B模型中，我们只是断开O—H 键，H还留在表面上。也即是B模型保持了与反应物分子相一致的原子种类以及数目。

这两个办法有什么区别呢？哪个更好些?

我们先分析下B)的模型：它比A模型多了一个H，可以认为H 吸附在A模型上；因此A中CH$_3$O的存在会对H的吸附能产生影响，一方面来源CH$_3$O对催化剂电子结构的影响，另一方面来自与空间的影响，类似于前面我们学习过的覆盖度对O原子吸附的影响。因此我们可以计算并对比H在纯净slab和A上面的吸附能。

$\Delta E{ads}$ =$E{ads}^{slab}$ -$E{ads}^{A}$ = [$E{H}$ - $E{Slab}$ - $E{H2}/2$] - [$E{CH_3O+H}$ - $E_{CH_3O}$ - $E_{H_2}/2$]

= ($E{H*}$ + $E{CH3O*}$) - ($E{Slab}$ + $E_{CH_3O+H}$)

A和B模型的区别为： 将$CH_{3}O$ 和 H 分离到无穷远时候的体系能量的变化。

再看一下A和B两个模型中反应热的计算：

A)模型：$\Delta$E(A) = $E{CH_3O*}$ + $E{H}$ - $E_{CH_3OH}$ - $E_{slab}$

B)模型：$\Delta$E(B) = $E{CH_3O + H}$ - $E{CH_3OH*}$

反应热的差：

$\Delta$E(A) - $\Delta$E(B) = $E{CH_3O*}$ + $E{H}$ - ($E{Slab}$ + $E{CH_3O+H*}$) = $\Delta E_{ads}$

通过上面的分析，我们得到同样的结果，即两个体系模型的区别主要在于产物之间的相互作用。如果产物之间相互作用弱，可以认为彼此相差甚远，互不影响，也就是A模型，这也是大部分人在计算过程中常常采用的方法。例子有很多，就不一一介绍了，随便取一个： ACS Catal. 2014, 4, 11, 4178–4188。有兴趣的可以去看看。

对于B模型，可以从表面覆盖度对反应的影响这一角度来分析，在键断裂后，如果产物与催化剂结合较强，来不及扩散至互不影响，那么局部的覆盖度就会增加，从而对后面的反应产生影响。有兴趣的可以参考一下这两篇文章：

ACS Catal. 2015, 5, 1, 104–112； ACS Catal. 2014, 4, 6, 1991–2005。

覆盖度对表面反应的影响很复杂，一般人也不愿意碰，但是在计算过渡态相关的操作过程中，B模型却发挥着重要的作用。可以从下面2个角度来分析：1）过渡态插点的技术角度 以及2）获取合理过渡态的角度。这些将会在下一节分析。