Ex33 晶格参数的确定(Birch-Murnaghan状态方程-1)
O$_2$分子的计算中,我们知道了,单纯从数据库中获取的结构,只能作为一个合理的初始值,与计算所得到的理论结构还有一定的差距,因此我们需要对该结构进行优化才可以获取稳定的晶格参数信息。有两个方法可以实现:
- 1 Birch-Murnaghan状态方程拟合,
- 2 VASP计算中通过调节ISIF参数直接优化Bulk。
下面两节我们先讨论一下第一个方法:BM方程拟合。
1 什么是Birch-Murnaghan方程?
BM方程为块体材料的体积随着外压变化的状态方程。大师兄参考了维基百科的说明,大家下载维基百科导出的PDF文件参考。在学习下面的内容前,请务必阅读这个文件,了解什么是Birch-Murnaghan方程。下载:http://pan.baidu.com/s/1bUSYbs


2 如何通过BM方程获取晶格参数?
首先,我们将BM方程中的体积转化为晶格参数(a)的函数:
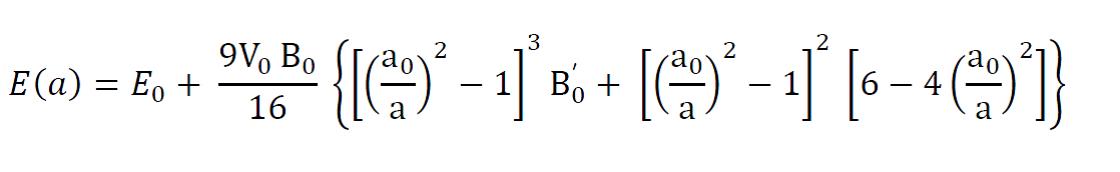
其中E(a)和E$_0$是晶格参数为a和a$_0$时bulk的能量,B$_0$,B$_0$’和V$_0$这些见BM方程的维基百科介绍。令$(1/a)^2 = x$,上图中的BM方程可以写成:
$y(x) = c_0 + c_1x + c_2x^2+c_3x^3 $ 的形式,
E$_0$, B$_0$,B$_0$’和V$_0$等写进c$_0$,c$_1$,c$_2$,和c$_3$这些常数里面,它们的具体形式此时并不重要,我们需要做的就是拟合这样的曲线去寻找使y(x)为最小值时的x取值。对y(x)这个方程求导数,dy(x)/dx = 0 的时候,便可以获取能量最低时的x值了,再由$(1/a)^2 = x$ 获得晶格参数。
dy(x)/dx = c$_1$+ 2c$_2$x + 3c$_3$x$^2$
令:dy(x)/dx = 0,即 c$_1$+ 2c$_2$x + 3c$_3$x$^2$ = 0
这是一个典型的二项式方程,求解很容易。
x有两个值,其中负值被舍弃掉,最终:
3 获取拟合的数据:
经过前面的分析,我们需要的就是获得的c$_1$,c$_2$ 和c$_3$值。可以设置一系列不同的晶格常数进行计算,得到对应的能量,然后将这些数据带入下面的方程中:$y(x) = c_0 + c_1x + c_2x^2+c_3x^3 $进行拟合。本节我们主要讨论一下如何进行该计算。看到这里,你第一反应是我们之前测试K点或者SIGMA值时的那些Linux批量操作。是的,我们也需要进行一个批量操作的计算。
3.1 分数坐标
如果我们改变了晶格常数,那么Fe原子的坐标也要发生相应的变化。此时,用分数坐标更加方便,VESTA中在cif转VASP格式的时候,会提醒你选择哪个形式的坐标,我们选择分数坐标:
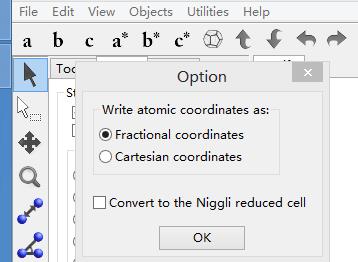
POSCAR如下图:
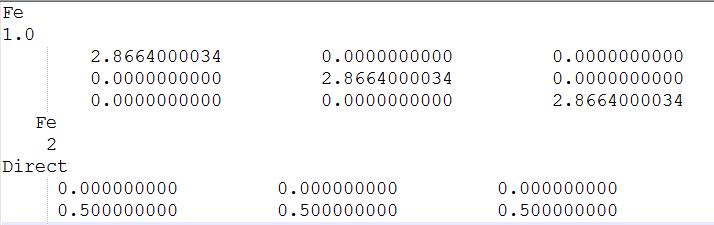
注意:
如果前面练习中,导出的为笛卡尔坐标形式的,你有两个选择:
A)重新按照前面的步骤,用VESTA导出为分数坐标形式;
B)将单点计算的结果直接复制过来(cp CONTCAR POSCAR),因为VASP的输出坐标为分数坐标形式,单点计算中,晶胞原子都没有动,CONTCAR可以直接使用。复制过来的POSCAR如下:
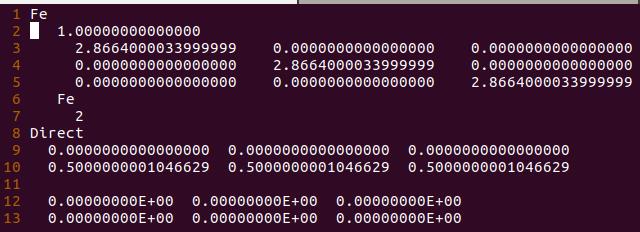
3.2 获得分数坐标的POSCAR后,我们可以批量对晶格常数a,b,c进行批量操作,也可以对缩放系数进行批量操作,而原子的坐标不用去管。
3.3 本练习对缩放系数进行批量操作
我们取10个点,将1.0 替换成0.95, 0.96, 0.97, 0.98, 0.99, 1.01, 1.02, 1.03, 1.04, 1.05。此时,晶格常数为:缩放系数*2.8664.(记住,下一节用得到)
a) 准备缩放系数为1.0 的计算文件夹,命名为1.00,里面包含我们前面一节已经讲过的Bulk单点计算相关文件;
b)
1 | for i in 0.95 0.96 0.97 0.98 0.99 1.01 1.02 1.03 1.04 1.05; do cp 1.00 $i ; sed -i "2s/1.0/$i/g" $i/POSCAR ; done |
注意:这里大师兄在自己电脑的~/.bashrc文件里面设置了:alias cp='cp -r'
思考: sed 命令后面用的是双引号(为什么?)如果这里看不懂的话,建议从Ex00开始学习。
d.) 批量提交命令:
1 | for i in *; do cd $i; qsub sub4; cd $OLDPWD; done |
其中,qsub sub4 是大师兄提交单个任务的命令。
3.4 数据提取:
1 | for i in *; do echo -e $i "\t" $(grep ' without' $i/OUTCAR | tail -n 1| awk '{print $7}'); done > data |
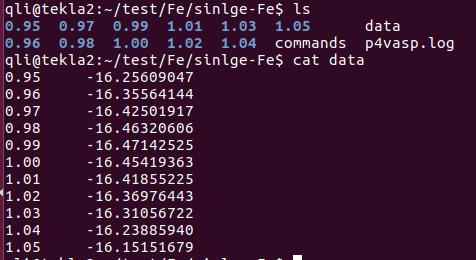
3.5 以上计算文件以及相关的命令已经上传到QQ群文件和百度网盘了,大家对比下计算结果。 http://pan.baidu.com/s/1dEJr9rb
4 扩展练习
4.1 完成本练习中的相关操作,并学习VASP官网批量操作的例子:
https://cms.mpi.univie.ac.at/wiki/index.php/Fcc_Si
注意:FCC Si的例子用的原胞,并且该网址最后图中曲线不是二次方程!!!虽然用二次方程拟合出来的结果差不多。
4.2 探索学习曲线拟合的方法;
4.3 学习并了解BM方程以及如何拟合,如何通过BM方程获取稳定的晶格参数;
4.4 对晶格参数进行批量操作,并计算。
5 总结
本节从BM方程开始,简单介绍了什么是BM方程,如何通过BM方程获取稳定晶胞对应的晶格参数,最后,又复习了一下本书前面几节的批量操作,下一节我们讲解一下如何通过python脚本对BM方程拟合。